Harry Partch explains just intonation (02:29)

Partch explains his version of just intonation, "monophonic" (01:08)

Partch compares tempered triads with true triads (01:22)

The Scale of Olympus (00:46)

The Scale of Archytus (00:58)

The Scale of Pythagoras (01:07)

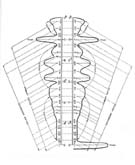
Standard tuning in today's Western classical music is called 12-tone equal temperament. The everyday scale that we use divides an octave into 12 equally spaced pitches. The major advantage to having equal temperament is that melodies can be transposed into any key and remain identical. A melody written in the key of C sounds the same as a melody written in the key of D, and so on. By the same token, every key sounds more or less the same, and the distinct characters of different modes are lost, along with their expressive potential.

Americans have heard equally spaced scales all our lives and have learned to accept them as normal. When we hear other scales, such as Asian, Indian, or Greek, they sound as if they are out of tune because they don't fit neatly into our preconceptions.

The 12-tone equal temperament system is actually a rather recent development in modern history. It has dominated in Western music for only about 250 years. Before that, pitches were devised by following the harmonic series that exists in nature, which is not equally spaced. Composers prior to 1750 wrote for unequal temperaments (and there were many tuning systems to choose from, including Pythagorean, mean-tone temperament, and well temperament). Many people are surprised to learn that Bach did not use today's 12-tone scale: His pieces originally sounded quite different from the monochrome colorings we now hear them in.

Just intonation was used as early as 5,000 years ago, and it uses intervals that are the smallest whole-number ratios of a fundamental pitch, such as 2/1, 3/2, or 4/3. Many of these small ratios are very close (but not identical) to significant pitches in our familiar 12-tone scale; after a certain point it makes no sense to translate them into letter equivalents and it is more accurate to refer to their precise number ratios. If the fundamental pitch is G (as it was in all of Harry Partch's instruments), a 4/3 ratio (a "fourth") is 2/100ths of a half-step short of a C; 3/2 is 2/100ths above a D. Twelve-tone equal temperament acknowledges that our ear is drawn to these pitches, but compromises perfect pitch in order to stay equally spaced. Many notes that appear in Partch's just-intonation system are as much as 50/100ths of a half-step off from pitches most Westerners are used to recognizing.

Composers such as Harry Partch, Lou Harrison, Terry Riley, Ben Johnston, and La Monte Young were more interested in getting back to these more resonant harmonies. For Harry Partch it meant that new instruments had to be built. For La Monte Young it meant retuning the piano or using pure sine waves to produce perfect harmonies. Lou Harrison looked to cultures that had already developed their own instruments. Henry Cowell designed his Rhythmicon to apply the same harmonic series to the proportions of rhythmic cycles; thus, duplet rhythm would correspond to an octave (2/1), triplets to a fifth (3/2), etc.

Partch's system is a logical extension of music history. Our ears gradually became used to higher numbers of the harmonic series being consonant: 3 in Medieval Europe, 5 in the Renaissance, 7 and 9 in jazz, 11 in Partch. This allows for 29 tonalities in Partch's system providing for modulation into 29 different keys (yes, Partch was a very "tonal" composer!) and a much wider range of consonance and dissonance than found in other systems. Secondary intervals are frequently added to these primary tones to make up the infamous "43 tone scale" for which Partch is unjustly famous.